The Lorentz transformation for star/neutrino movements
If one applies the Lorentz transformation on the following set-up, the results turn out to be very peculiar.
Two stars emit neutrinos, e.g. the sun (-> neutrino 1) and Proxima Centauri (-> neutrino 2).
We observe these neutrinos, both of which are moving away from their star at 99.99% the speed of light.
They maintain their speed as they approach each other.
The two neutrinos do not experience any acceleration on their way through space. According to Einstein's theory of relativity:
Each can be viewed as resting.
The objects in their environment can be calculated as moving relative to them.
In order to put this consideration into a real framework without an object exceeding the speed of light, according to Einstein's theory of relativity, the speed of other objects is recalculated using the Lorentz transformation,
according to the principle
![]()
and the formula
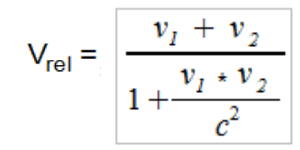
A) For us as objective viewers it is clear:
In a minute, Neutrino 2 will hit the sun.
In half a minute, Neutrino 2 will meet Neutrino 1.
B) From the point of view neutrino 2, which considers itself to be at rest:
- Neutrino 2 sees both the sun and neutrino 1, which is emitted by the sun right now, approaching at breakneck speed.
- The Lorentz transformation results in the following velocities of the surrounding objects for neutrino 2:
B1) Speed of the sun in relation to neutrino 2:
VSun ~ 0
VNeutrino2 = 0.9999 * c
=> The resting neutrino 2 sees the sun approaching with 0.9999 * c.
This corresponds to the expectation and also to the Galilean transformation: the other object takes over your speed if you consider yourself to be at rest.
B2) Velocity of neutrino 1 in relation to neutrino 2
VNeutrino1 = 0.9999 * c = 299'762'479 km/s
VNeutrino2 = 0.9999 * c = 299'762'479 km/s
c = 299'792'458 m/s
The result corresponds to the expectation of the Lorentz transformation: nothing moves faster than light, not even relatively.
The consequence of this is that both neutrino 1 and the sun move towards neutrino 2 at virtually the same speed. Instead of within half a minute for neutrino 1, they will both reach neutrino 2 in one minute with an extremely minimal time gap.
This seems impossible. Applying a Lorentz transformation at low speeds, the reuslt seems to correspond to the Galilean transformation. Applied for high speeds, the Lorentz transformation seems to create a reality that is not possible.
How could this be possible for two objects, moving at such different speeds from the same starting point and starting time, to reach a third object at almost the same time?
It becomes even more obvious with photons i.e. with electromagnetic waves: They move towards each other at the speed of light before they cross each other. Relative to each other, they move and cross at twice the speed of light, without hurting the law of nature not to move faster than at light speed.
Am I concluding correctly?
The Lorentz transformation does not allow this natural, relative encounter and crossing speed vrel.max. = 2c, although none of the objects moves faster than light.
Therefore with high speeds, the Lorentz transformation leads to realities that are impossible?
Does the success of Einstein's general theory of relativity lie among other things in the correct prediction of the curvature of space, which remains true even without relativity, just like correctly performed vector field calculations can be made without applying the Lorentz transformation?
Did a fundamental error of applying the Lorentz transformations remain undiscovered for so long, because at speeds that are not extremely high (below approx. 10% of light speed / 30,000 km/s) it is very close or equal to the Galilean transformation?
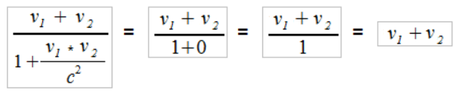





Kommentare
Kommentar veröffentlichen